8-8÷8+8 = கேள்வி இது என்னுடைய ஒழுங்கு (8-(8 ÷8))+8 [8-1+8 = 15 பதில்]
↓ → Arithmetic Bodmas Low
(. ) bracket
x² Order
÷ division
× Multiplication
+ Addition
- Subtraction
ஒரே தன்மையான கணக்குகள் இடமிருந்து வலமாக செல்லும் ➡
மேற்கோள்: ((5×3)-2)+1×2 [13 + 2 =15✓ பதில்]
எனக்கு கணக்கு பாடம் நல்லா தெரியும் என்று கிடையாது, ஏதோ கொஞ்சம் கற்றுதெரிந்து வைத்திருக்கின்றேன். தரையில் அமர்ந்து கொண்டு நீச்சல் அடிக்க முடியாது. கடலில் இறங்கித்தான் ஆக வேண்டும். நான் கூட கணக்கு பாடத்தில் மூழ்கித்தான் எழுந்திருக்கிறேன். இணையத்தில் இது போன்ற கணக்குகள் எக்கச்சக்கமாக வந்து கொண்டிருக்கின்றது.
இருப்பினும் பதில்கள் பாதிக்கு மேல் தவறானது. அவர்கள் எண் கணக்கு விதிகளை எதையும் பயன்படுத்தாமல் வெறும் தந்திரம் [Trick] பயன்படுத்தி கணக்கு செய்கிறார்கள். பள்ளிகளில் இது போன்றுதான் கற்றுக் கொண்டிருக்கிறார்களா....? இப்படி நீங்கள் கற்றால் அது வெறும் ஏட்டுச் சுரக்காய், உங்களால் ஒரு அப்பளம் கூட சுட முடியாது.
எண்கணிதமும் தமிழும் ஆங்கிலமும் பொதுவில் சொன்னால் பெரும்பாலான மொழிகள் இடமிருந்து வலமாக வாசிக்கப்படும். அரபு மற்றும் ஹீப்ரு ஆகிய மொழிகள் வலமிருந்து இடப்புற மொழிகளாகும். இருப்பினும் எண்கணிதம் பொது விதிக்கு உட்பட்டு வாசிக்கப்படுகின்றது அவங்க வலமிருந்து இடமாக கணக்கு பார்த்துவிட்டு தங்களுடைய பதில் சரி என்று சொல்கிறார்கள்.
நீங்கள் PEMDAS, BODMAS, BOMDAS அல்லது வேறு ஏதேனும் வழிமுறைகளை பயன்படுத்தினாலும் பரவாயில்லை, அவை இன்னும் கணித ஓடர் செயல்பாட்டின் அடிப்படைக்கு வருகின்றது. அடைப்புக்குறிக்குள் இல்லாதது சமன்பாட்டை அவை தெளிவற்றதாக ஒரு போதும் மாற்றாது, ஏனெனில் அவை முதன்மையாக சமன்பாட்டின் ஒரு பகுதியை மற்றொன்றுக்கு முன்னதாக முடிக்கப்பட வேண்டும் [கணக்கிடபட வேண்டும்] என்பதைக் குறிக்கப் பயன்படுத்தப்படுகின்றன.
அடைப்புக்குறிகள்/அடைப்புக்குறிகள் முதலில் முடிக்கப்படும். இந்த சமன்பாட்டில் எதுவும் இல்லாததால், நீங்கள் விதிகள் இரண்டிற்கு செல்கிறீர்கள். அடுக்குகள்/ஆர்டர்கள் இரண்டாவதாக முடிக்கப்படும். இந்த சமன்பாட்டில் எதுவும் இல்லாததால் நீங்கள் விதி மூன்றில் செல்லுங்கள். →
பெருக்கல்/வகுத்தல் சம அடிப்படையில் செய்யப்படுகின்றது. அவர்கள் சந்திக்கும் போது இடமிருந்து வலமாக வேலை செய்கிறார்கள்.[கணக்கிடுகின்றது] கூட்டல்/கழித்தல் கடைசியாக மற்றும் சம அடிப்படையில் செய்யப்படுகின்றது.
மீண்டும் அவை நிகழும் வரிசையில் இடமிருந்து வலமாக வேலை செய்கின்றன. 17 ஆம் நூற்றாண்டின் நடுப்பகுதியில் இருந்து இந்த செயல்பாட்டு வரிசை பரவலாக ஏற்றுக்கொள்ளப்பட்டது. எல்லா நாடுகளிலும் இதுதான் பயன்பாட்டில் இருக்கின்றது.
மேற்கோள்: f(8x^2) dx = 64/3 (f 0 > 2) கணக்கலகு [கால்குலேட்டர்] ஒரு கருவி அதில் எதை பதிவிடுகிறார்களோ அதை அது பதிலாக தரும். தவறாக ஒரு கணக்கை எழுதினால் அது தவறாகத்தான் பதிலை தரும். சரியான வழிமுறையை பயன்படுத்தினால் மட்டும்தான் அது சரியான பதிலைத் தரும்.
என்னுடைய கணக்கு தப்பு என்றால் நீங்கள் ஏதாவது வழிமுறை வைத்திருக்கிறீர்களா இருந்தால் சொல்லுங்கள்.
BODMAS உருவாக்கியவர் யார்? கணிதச் சிக்கலைத் தீர்ப்பதற்கு, உதவுவதற்காக அக்கிலிஸ் ரீசெல்ஃபெல்ட் என்பவரால் BODMAS அறிமுகப்படுத்தப்பட்டது. [1700-1800] கணிதவியலாளர் அகில்லெஸ் . இது ஒன்றுக்கு மேற்பட்ட கணித செயல்பாடுகளை உள்ளடக்கிய ஒரு கணித அறிக்கையில் கணித ஆபரேட்டர்களை எவ்வாறு மதிப்பிடுவது என்பதை நினைவில் கொள்ள உதவும் நினைவாற்றல் ஆகும்.
சமீபத்தில் இணைய சமூகத்தை பைத்தியக்காரத்தனமாக வழிநடத்தும் ஒரு சில கணிதச் சிக்கல்களை பதிவிடுகின்றனர் . முதல் பார்வையில், இது மிகவும் எளிமையானதாகத் தெரிந்தாலும். கூர்ந்து கவனித்தால் அது தலைவலியாக மாறிவிடும்.
போட்மாஸ் அமெரிக்கா, இங்கிலாந்து, பாகிஸ்தான், இலங்கை, இந்தியா, பங்களாதேஷ் மற்றும் ஆஸ்திரேலியா மற்றும் பிற ஆங்கிலம் பேசும் நாடுகளில் மிகவும் பொதுவானது BODMAS ஆகும், அதாவது அடைப்புக்குறிகள், ஒழுங்கு , வகுத்தல்/பெருக்கல், கூட்டல்/கழித்தல் அல்லது அடைப்புக்குறிகள், மூலம்/வகுத்தல்/பெருக்கல், கூட்டல்/கழித்தல். அரபு, நைஜீரியா மற்றும் சில மேற்கு ஆப்பிரிக்க நாடுகளும் BODMAS ஐப் பயன்படுத்துகின்றன.
↓ → Arithmetic Bodmas Low
(. ) bracket
x² Order
÷ division
× Multiplication
+ Addition
- Subtraction
இந்த ஒழுங்கை நீங்கள் நினைவில் வைத்திருந்தாலே போதுமானது.கணக்கு பாடம் தானாக வரும். போட்மாஸ் அல்லது பெம்தாஸ் இதில் எது சிறந்தது? கணிதக் கணக்கீடுகளில் நாம் BODMAS அல்லது PEMDAS ஐப் பின்பற்ற வேண்டுமா? இதில் எது வேண்டும் என்றாலும் பரவாயில்லை, நீங்கள் எதை வேண்டுமானாலும் பின்பற்றுங்கள்
ஆனால் அதனுடைய ஒழுங்கு மட்டும் மிக முக்கியம். PEMDAS மற்றும் BODMAS இரண்டும் வகுத்தல் மற்றும் பெருக்கத்தை ஒரு படியாகக் கணக்கிடுகின்றன. இறுதி விதி இடமிருந்து வலமாக செல்ல வேண்டும் என்பது கணக்கின்விதி மற்றும் இன்னும் ஒரு விதி. [கழித்தல்/கழித்தல் ] = கூட்டல் [கூட்டல்/கழித்தல்] = கழித்தல் இதையும் நீங்கள் கவனத்தில் கொள்ள வேண்டும்.
பயிற்சி மேற்கோள்:
1) 9+9-9×9+9 ? கேள்வி
செய்முறை: 9+(9-(9×9))+9
9+ (-72 ) + 9. [ - - ] = +. [ - + ] = -
→ 18+ (- 72) = -54 பதில்
2) 5-9÷3+8 ? கேள்வி
5-((9÷3)+8) = -6 தவறான கணக்கீடு
→ (5-(9÷3))+8 = 10 ✓ பதில்
எண்கணித விதி தகைமை [faculty]
0! = 1
1! = 1
2! = 2 [1×2]
3! = 6 [1×2×3]
4! = 24 [1×2×3×4]
5! = 120 [1×2×3×4×5]
6! = 720 [1×2×3×4×5×6]
7! = 5040 [1×2×3×4×5×6×7]
8! = 40320 [1×2×3×4×5×6×7×8]
9! = 362880 [1×2×3×4×5×6×7×8×9]
1) மேற்கோள்: (1+4!)-(20-!) (1+24)-(20-1) 25 - 19 = 6
2) மேற்கோள்: 25-5÷5 இந்த கணக்கில் நான்கு பதில் a) -4, b 4, C) 4! d) 24
25-(5÷5) = 24 சரியான பதில் [ C) 4! ]
ஒருங்கிணைப்பு கணக்கீடு [கால்குலஸ்]: ஒருங்கிணைந்த கால்குலஸ் பகுப்பாய்வின் ஒரு பகுதியாகும். இது பரப்பளவு மற்றும் அளவைக் கணக்கிடப் பயன்படுகின்றது. மற்றும் வின்வெளி ஆய்வு கணக்கிடவும் பயன்படுகின்றது. இதுவொரு பெரிய பாடம், சுருக்கமாக கணக்கலகு [கால்குலேட்டர்] எப்படி கணக்கீடு செய்வது அதைமட்டும் சொல்லித்தாறேன்.
நீங்கள் ஒரு கருவியை, சாட்டிலைட் உதிரிப்பாகம் ஒன்றை செய்கிறீர்கள் அதில் ஒரு பரப்பளவு, வட்டம், சதுரம் அல்லது முக்கோணமாக இல்லாமல் சற்று நெளிந்து கோணலாக இருந்தால் அந்த மேற்பரப்பை அளவிட இந்த ஒருங்கிணைப்பு கணக்கீடு பயன்படுகின்றது அதனுடைய Formel: f(X)= X மேற்கோள்: f(8x^2) dx = 64/3 (f 0 > 2)
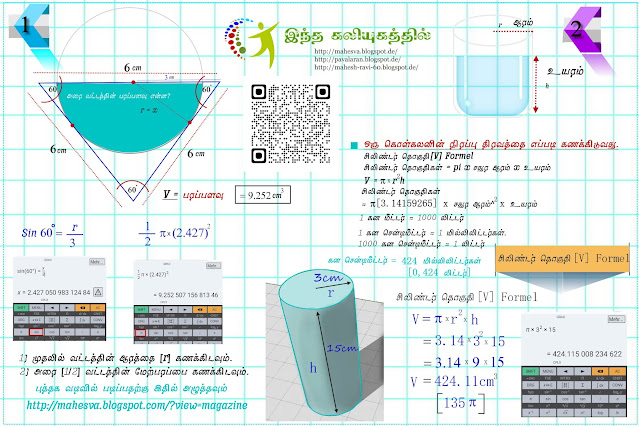
ஒருங்கிணைந்த கணக்கீடு[integral calculus] அற்புதமான ஒரு கணக்கு. இது எதற்கெல்லாம் பயன்படுகின்றது. இது சிக்கலான வடிவங்களின் பரப்பளவு மற்றும் அளவைக் கணக்கிடப் பயன்படுகின்றது.சிக்கலான வடிவம் revolution உடல்களுக்கான தொகுதி கணக்கீடு முறை [ஃபோர்மல்] ஒரு புரட்சியின் அளவைக் கணக்கிடுவதற்கான Formel : V = π ⋅ ∫ a b ( f ( x ) 2 d x
மேற்கோள்: f(x)= √x+6 .. மேலே x∈ [-6;2] ஒருங்கிணைப்பைப் பயன்படுத்தி தொகுதி கணக்கிடப்படுகின்றது V=π⋅∫ [−6 2] ( x+6 )2⋅dx = 32π பதில்
மடக்கை விதிகள் [Log]( Rregullat logaritmike): இது 1728 இல் லியோன்ஹார்ட் ஆய்லரால் [1707 -1728] இடைப்பட்ட ஆண்டில் தீர்மானிக்கப்பட்டு, 1742 இல் முதன்முதலில் இந்த கணித விதிகள் வெளியிடப்பட்டது. இது மடக்கையின் அடிப்படை விதியாக பயன்படுத்தப்படுகின்றது,மற்றும் இது இயற்கை மடக்கை என்றும் அழைக்கப்படுகின்றது. இந்த விதிகளை கணக்கலகு, கால்குலேட்டரைக் கொண்டு எப்படி கணக்கிடுவது. சின்ன உதாரணங்களுடன் சொல்லி தாரேன். இந்த அடிப்படை விதிகளை கொண்டுதான் கால்குலேட்டர் இயங்குகின்றது.
மேற்கோள்: 1
2^x =16. X= ? [2×2×2×2] = [2^4=16]
Log(16) ÷ Log(2) = 4✓
அடுக்கு மற்றும் அடிப்படை இரண்டையும் கணக்கிடுவது.
Log2(16) = 4 [2^x]
Log4 (16) = 2 [x^2]
மேற்கோள்: 2
(1/3)^m = 1/81.
m = ? 4 பதில்
Log2,(1/81) ÷ Log2,(1/3) = 4
n^2 = 64
n = ? 6. பதில்
Log(64) = 6
m × n = [4×6] = 24 ✓
2) X= ?
8^x = 64
Log(64) ÷ Log(8) = 2✓
மேற்கோள்: 3) கேள்வி: y = ?
3y+6 = y+12 பதில் y=3
மேற்கோள்: 4) கேள்வி: x = ?
2^x+3 = 16 [log2^16 = x+3 பதில் x = 1
மேற்கோள்: 5) கேள்வி: x = ?
2^x = 64 [log2^64 = x
பதில் x = 6 [2x2x2x2x2x2] = [2^6]
மேற்கோள்: 6) கேள்வி: x = ?
2^x2=4^x [log2^(4) = 2 பதில் x = 2
கேள்வி: 9-3 ÷ 1/3 + 1 இந்த கணித சிக்கலை எவ்வாறு தீர்ப்பது? இந்த புதிர் 1980 களில் முதலில் ஜப்பானில் வெளியிடப்பட்டது . என்னைப் போன்று 70-80 களில் பள்ளியில் கல்வி கற்றவர்களுக்கு இந்த கணக்கிற்கு விடை காணும் திறன் இருக்கும். மீண்டும் இந்த கணக்கு இணையதளங்களில் வயர்லாகி வருகின்றது. தற்செயலாக என் கண்ணில் பட்டது. அதை என்னுடைய ஸ்பெஷலாக எடுத்துக் கொண்டேன்.
கணக்கின் ஒரு பகுதி வகுத்தால் புள்ளி கணக்கீடு திடீரென்று முற்றிலும் மாறுபட்டமுடிவைக் கொண்டுள்ளது. வகுத்தல் பெருக்கலாக மாறுகின்றது . கணிதத்தில் இதுபோன்று பல விதிகள் விதிகளாகவே இருக்கின்றன. இது போன்ற கணக்குகளில் எந்தமாற்றமும் செய்ய முடியாது. அதை அப்படியே ஏற்றுக்கொள்ள வேண்டியதுதான்.
பழைய கால்குலேட்டரைக் கொண்டு கணக்குப் பார்த்தால் 9-3÷1÷3+1=9 என்ற பதிலைதான் தரும். செய்முறை: 9-(3÷(1/3))+1 பதில் =1✓
9-9+1 [3÷(1/3) = 9 ]
[3÷1= 3×3 =9]
கேள்வி : 99-((99×99)×0) நீங்கள் எந்த இலக்கத்துடன் [ × 0] = 0 பெருக்கினாலும் அந்த இலக்கம் ஜீரோவாக மாறிவிடும். பதில்: 99
சதுரம் மற்றும் முக்கோணத்தின் சுற்றளவு / மேற்பரப்பை கணக்கிடுதல்.
மேற்பரப்பு Formel: A = a × b [cm2] = 7 × 5 cm2
சுற்றளவு Formel: U = 2 × a + 2 × B.[cm] = 2 × 7+2 × 5 =24cm
முக்கோணத்தின் சுற்றளவு Formel: U =1/2 2 × a + 2 × B.[cm] = 2 × 7+2 × 5 =24cm [24/2 = 12 cm முக்கோணத்தின் பிரதியாக இன்னுமொரு முக்கோணத்தை வரைந்து சதுரத்திலிருந்து பாதியை கணக்கிட்டு கொள்ளலாம்.
கேள்வி: -10^2+100=?
பதில்: (-10×10)+100
-100+100 = 0 ✓
கவனத்தில் கொள்ள:
-100+100 = 0
-100 -100 = -200
-100÷100 = -1
-100×100 = -10,000
-100 - (-100) = 0
2x-3÷3+4^0 கேள்வி
(3÷3)+1
2x - 1+1 = 2x✓
4^(0) = 1
40^(0) =1
400^(0) =1
எந்த இலக்கத்தின் மேல் 0 வந்தாலும் அந்த எண் 1 என்று மாறிவிடும்.
நீங்கள் எந்த இலக்கத்துடன் [ ? × 0] = 0 பெருக்கினாலும் அந்த இலக்கம் ஜீரோவாக மாறிவிடும்.
15-25= -10 சிறிய இலக்கத்தை பெரியதை கழித்தால் அது மைனஸ் ஆக மாறும் (-)
25-15 =10
கேள்வி: 36÷4+5^2-2×6
((36÷4)+5^2)-(2×6)
(9+25) -12
பதில் 34-12 =22✓
50÷2(2+3) கேள்வி
25 × 5 = 125
அவர்கள் தந்த பதில்கள்:
a) 120, b) 100, c) -125 d) 5
= 3√125 = 5✓
கேள்வி: 4!×5!/4!+5!+100
அவர்கள் தந்த பதில்கள்:
a) 120, b) -120, c) -125 d) 5!
பதில் = 5! [5×4×3×2×1] = 120
கேள்வி : 36÷(6÷18)×12^-1+6
செய்முறை: (36÷(6÷18)×1÷12+6
((108×1) ÷12)+6
பதில்: 9+6=15
கேள்வி : 99-((99×99)×0) நீங்கள் எந்த இலக்கத்துடன் [ ? × 0] = 0 பெருக்கினாலும் அந்த இலக்கம் ஜீரோவாக மாறிவிடும். பதில்: 99
கேள்வி: X÷3+5=12. X=?
(21÷3)+5. [7+5 =12]
பதில் : X = 21
கேள்வி: 4-4×3+14
(4-(4×3))+14
-8+14 = 6✓ பதில்
-1-(4^2)= கேள்வி
-1-(-16)=15✓
ரூட் √ என்பது இரண்டு மதிப்புள்ள செயல்பாடு.
!√-1 ? கேள்வி
! =1 [1√-1 = -1] பதில்
ஒரே தன்மையான கணக்குகளை இடமிருந்து வலமாக படிக்கவும்.
கேள்வி 6+8(9-3)
செய்முறை: 6+(8(9-3))
(8×6) = 48
6+48= 54✓
கேள்வி: 5×5÷5(1+4) இது போன்று அசல் கணக்கில் அடைப்பு குறி போட்டு இருந்தால் அது பெருக்கலை குறிக்கும்.
செய்முறை ((5×5)÷5)(1+4)
(25÷5) 5
5×5 = 25✓ பதில்
நீங்கள் நினைப்பது போல் இந்த கணக்குகளில் எந்த சிக்கலும் இல்லை. சாதாரண ஒரு மூன்றாம் வகுப்பு கூட்டல் கணக்குகள். கணக்குகளுக்கான விதிகளை நீங்கள் மனதில் வைத்திருந்தாலே போதுமானது. இது போன்ற கணக்குகளை வெகு சுலபமாக செய்துவிட முடியும்.
இயற்கணிதம் [எப்போதும் மாறி இருக்கும்.]
மேற்கோள்: X^X^3= 27 கேள்வி x ≈ 1.785 பதில் [ X = மாறி (variable)]
சமன்பாடு ஒரு சார்பு மாறியாக உள்ளது
1). z=f(x,y). 2). (A= a×b)
மேற்கோள்: 2^x =16. [2×2×2×2] = [2^4=16]
X= ? [Log(16) ÷ Log(2) = 4✓]
எண்கணிதம் [மாறி இல்லாமல்.] எண்கள் கூட்டல் கழித்தல் பெருக்கல் வகுத்தல் அடிப்படையாகக் கொண்டது.
மேற்கோள்: (2+4)6÷2 = கேள்வி ((2+4)×6)÷2
36÷2 = 18✓ பதில்
↓ → Arithmetic Bodmas Low
(. ) bracket
x² Order
÷ division
× Multiplication
+ Addition
- Subtraction
இயற்கணித சின்னங்கள்
x x மாறி
= சமமான அடையாளம்
≠ சம அடையாளம் இல்லை
≡ சமநிலை i
≜ வரையறைக்கு சமம்
:= வரையறையின்படி சமம்
~ தோராயமாக சமம்
≈ தோராயமாக சமம்
∝ விகிதாசார மாறிலி
∞ முடிவிலி சின்னம்
≪ மிகவும் குறைவாக
≫ மிகவும் பெரியது
() அடைப்புக்குறிகள் கணக்கிடுகின்றன
[ ] அடைப்புக்குறிகள் கணக்கிடுகின்றன
{ } பிரேஸ்கள்
⌊x⌋ தரை அடைப்புக்குறிகள்
எக்ஸ்! ஆச்சரியக்குறி
| x | செங்குத்து பார்கள்
f (x) செயல்பாடு
(f ∘g) செயல்பாடு கலவை
(a,b) திறந்த இடைவெளி
[a,b] மூடிய இடைவெளி
∆ டெல்டா மாற்றம்
∆ பாகுபாடு
∑ சிக்மா
http://mahesva.blogspot.com/?view=magazine










கருத்துகள் இல்லை:
கருத்துரையிடுக